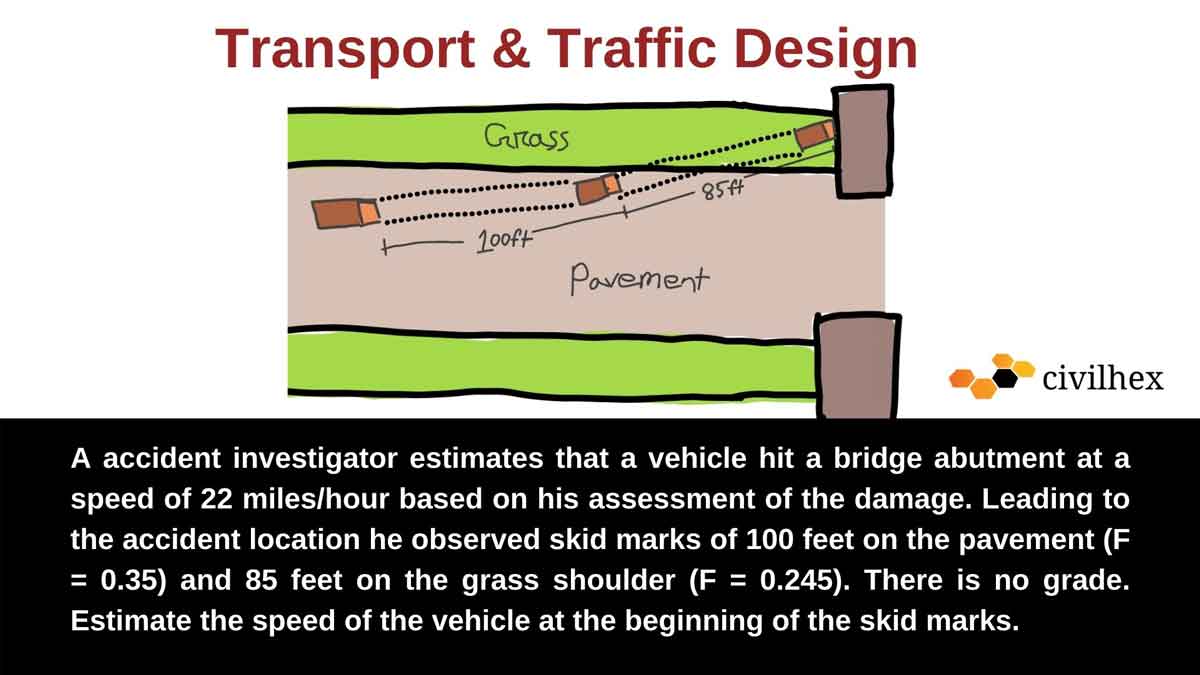
An accident investigator estimates that a vehicle hit a bridge abutment at a speed of 22 miles/hour based on his assessment of the damage. Leading to the accident location he observed skid marks of 100 feet on the pavement (F = 0.35) and 85 feet on the grass shoulder (F = 0.245). There is no grade. Estimate the speed of the vehicle at the beginning of the skid marks.
Transport & Traffic Design-A Accident Investigation Problem
Solution:
Given:
{{V}_{f}}=22\text{ miles/hr} \\ {{d}_{b\text{ }(pavement)}}\text{=100 feet and }F=\text{ }0.35 \\ {{d}_{b\text{ }(grass)}}=\text{85 feet and }F=\text{ }0.245 \\ \text{Now} \\ {{d}_{b\text{ }(grass)}}=\frac{{{V}_{i}}^{2}-{{V}_{f}}^{2}}{30(F)} \\ \Rightarrow 85=\frac{{{V}_{i}}^{2}-{{22}^{2}}}{30(0.245)} \\ {{V}_{i\text{ }(grass)}}=33.30\text{ miles/hr} \\ \text{Again,} \\ {{d}_{b\text{ }(pavement)}}=\frac{{{V}_{i}}^{2}-{{V}_{f}}^{2}}{30(F)} \\ \Rightarrow 100=\frac{{{V}_{i}}^{2}-{{33.30}^{2}}}{30(0.35)}\text{ }\to \text{ }\because \text{ }{[{V}_{i(grass)}}={{V}_{f(pavement)}]} \\ \therefore {{V}_{i(pavement)}}=46.46\text{ miles/hr}The speed of the vehicle at the beginning of the skid marks is 46.46 miles/hr.