Beam Design - Tension Reinforcement (Unknown Cross-Section) ACI 318-19

Beam Design – Tension Reinforcement (Unknown Cross-Section) ACI 318-19

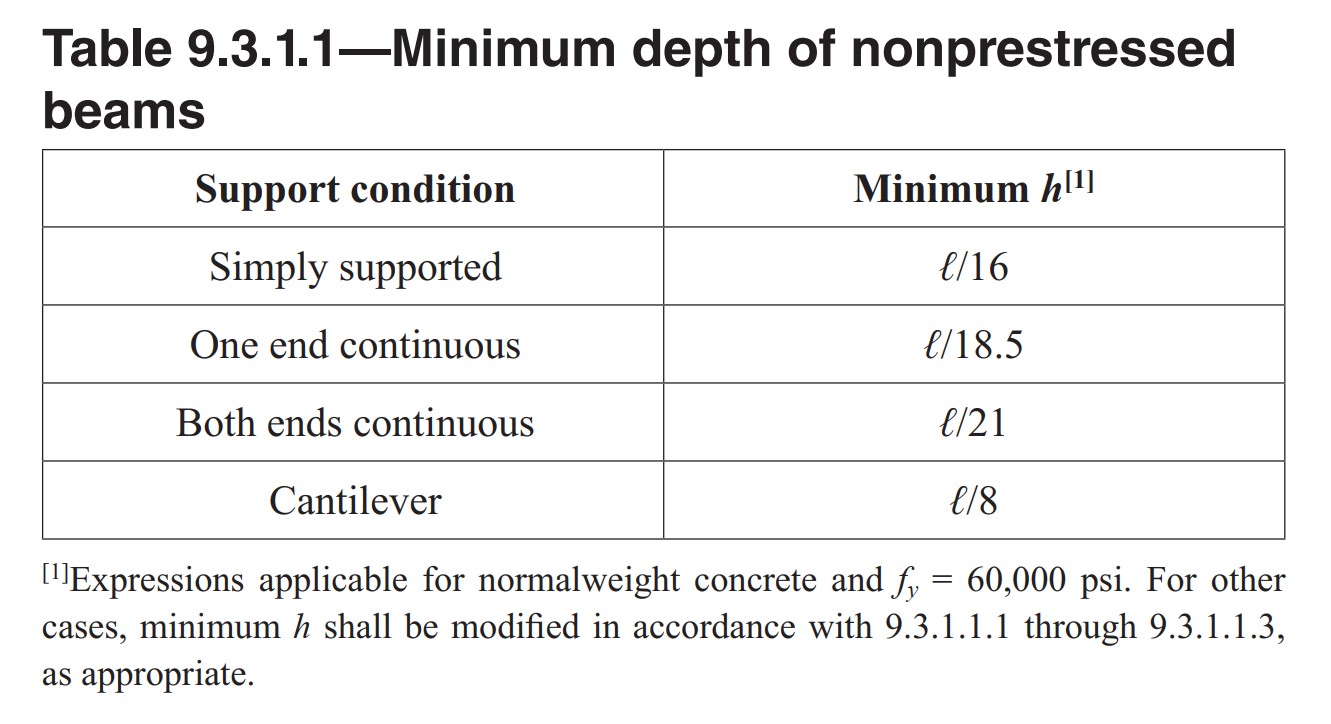
In this article, you going to learn about beam design, how to calculate the area of tension reinforcement in a beam and how to determine a beam-unknown cross-section by using ACI 318-19 design code. We also give a beam design example for better understanding and also gave beam design formulas with reference. Step 1: Minimum depth of nonprestressed beams: (ACI Table 9.3.1.1) Step 2: Ultimate Load: W_u Step 3: Ultimate Moment: M_u

\tag{4.26d} {{\rho }_{\max }}=0.85{{\beta }_{1}}\frac{f_{c}^{'}}{{{f}_{y}}}\frac{{{\varepsilon }_{u}}}{{{\varepsilon }_{u}}+{{\varepsilon }_{t,\min }}}

Step 5: Calculate bd² from Nominal Moment: $\phi {{M}_{n}}=\phi \rho {{f}_{y}}b{{d}^{2}}\left( 1-0.59\frac{\rho {{f}_{y}}}{f_{c}^{'}} \right) (4.34)$

Step 6: Find the trial size of the beam

Step 7: Calculate the area of steel

Step 8: Check for 𝜙 = 0.9

Step 9: Rebar calculation & Detailing

Beam Design Example for Unknown Cross-section as per
ACI 318-19:

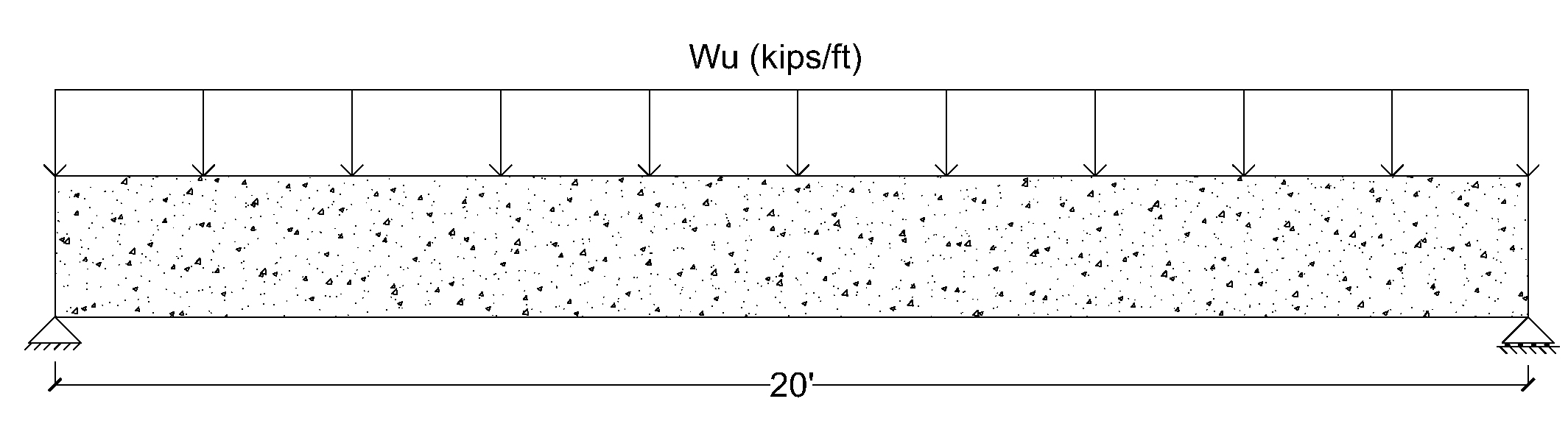
Find the concrete cross-section and the steel area required for a simply supported rectangular beam with a span of 20 ft that is to carry a calculated dead load of 1.5 kips∕ft and a service live load of 2.6 kips∕ft, as shown in Figure below. Material strengths are fc′ = 4000 psi and fy = 60,000 psi.

Table of Contents

Solution
Reference

Solution

Given,

L = 20 ft
Dead Load = 1.5 kips/ft
Live Load = 2.6 kips/ft
Unit weight of concrete, γ_c = 150 pcf (lb/ft³)
f’c = 4000 psi
fy = 6000 psi
β₁= 0.85

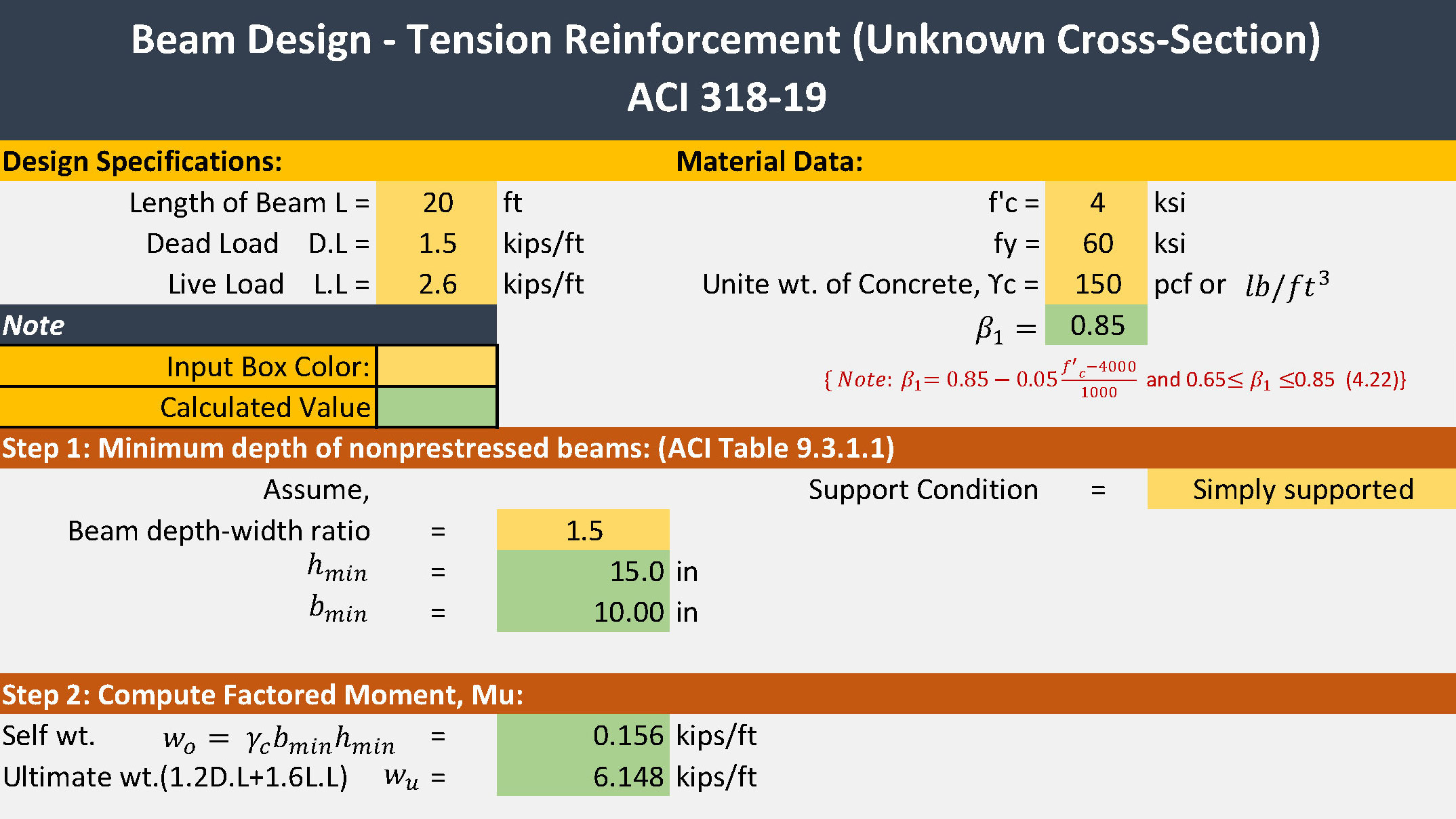
Step 1: Minimum depth of nonprestressed beams: (ACI Table 9.3.1.1)

Table 9.3.1.1—Minimum depth of nonprestressed beams

Assume, Beam depth-width ratio = 1.5 (h/b=1.5)

h_min= L/16 = (20*12)/16= 15 inch
b_min= 15/1.5 = 10 inch

Step 2: Ultimate Load: W_u

Self-weight W_o = ${{\gamma }_{c}}*{{h}_{\min }}{{b}_{\min }}=150\left( \frac{15}{12} \right)\left( \frac{10}{12} \right)=156.25lb/ft=0.156kips/ft$

Ultimate load
W_u = 1.2DL + 1.6LL = 1.2(w_o+DL)+1.6LL
= 1.2(0.156+1.5)+1.6(2.6)
W_u = 6.147 kips/ft

Step 3: Ultimate Moment: M_u

For simply supported beam
Maximum moment M_u:

\begin{align} & {{M}_{u}}=\frac{{{W}_{u}}{{L}^{2}}}{8}=\frac{(6.147){{(20)}^{2}}}{8} \\ & {{M}_{u}}=307.35kips-ft \\ \end{align} \tag{}

Step 4: Reinforcement ratio:

\begin{align} & {{\rho }_{\max }}=0.85{{\beta }_{1}}\frac{f_{c}^{'}}{{{f}_{y}}}\frac{{{\varepsilon }_{u}}}{{{\varepsilon }_{u}}+{{\varepsilon }_{t,\min }}} \\ & \to {{\rho }_{\max }}=0.85*0.85*\frac{4}{60}*\frac{0.003}{0.003+0.005} \\ & \to {{\rho }_{\max }}=0.0180 \\ \end{align} \tag{}

Note: Mobile users must use desktop mode to view equations correctly.

For Economy Use 60%-80% of the maximum reinforcement ratio. This is required for Underenforcement beam design.

{{\rho }_{design}}=0.8*{{\rho }_{\max }}=0.0145

Step 5: Calculate bd² from Nominal Moment:

\phi {{M}_{n}}=\phi \rho {{f}_{y}}b{{d}^{2}}\left( 1-0.59\frac{\rho {{f}_{y}}}{f_{c}^{'}} \right)

\tag{}\begin{align} & {{M}_{u}}=\phi {{M}_{n}} \\ & 307.35*12=0.9*0.0145*60*b{{d}^{2}}\left( 1-0.59\frac{0.0145*60}{4} \right) \\ & \therefore b{{d}^{2}}=5403.79i{{n}^{3}} \\ \end{align}

Step 6: Find the trial size of the beam

Used,

d = 1.5b
d²= 2.25b²(Square both side)
bd²= 2.25b³ (both sides multiply by b)

Now,
2.25b³= 5403.79 in³
b = 13.4 inch
So, d= 1.5b= 1.5*13.4 = 20.1 inch

So, trial size of the beam

b = 13.4 inch
d = 20.1 inch

Note: You can assume b=14 in & d=20.5 in for more practical usages. For this example, we are using it as it is.

Step 7: Calculate the area of steel

{{A}_{s}}={{\rho }_{design}}bd=0.0145*13.4*20.1=3.90\text{ }i{{n}^{2}}

Minimum flexural reinforcement (ACI 9.6.1.2):

{{A}_{s,\min }}\text{ larger of }\left\{ \begin{matrix} \frac{3\sqrt{f_{c}^{'}}}{{{f}_{y}}}{{b}_{w}}d=0.85\text{ i}{{\text{n}}^{\text{2}}} \\\\ \frac{200}{{{f}_{y}}}{{b}_{w}}d=0.90\text{ i}{{\text{n}}^{\text{2}}} \\ \end{matrix} \right. \tag{4.37a}

\therefore {{A}_{s,\min }}=0.90\text{ i}{{\text{n}}^{2}}\text{ OK}\text{.}

Note: $f_{c}^{'}\text{ and }{{f}_{y}}$ must be in psi.

Step 8: Check for 𝛟 = 0.9 (tension control)

a=\frac{{{A}_{s}}{{f}_{y}}}{0.85f_{c}^{'}b}=\frac{3.90*60}{0.85*4*13.4}=5.13\text{ in} \tag{4.28}

c=\frac{a}{{{\beta }_{1}}}=\frac{5.13}{0.85}=6.03\text{ in}

{{\varepsilon }_{t}}={{\varepsilon }_{u}}\frac{d-c}{c}=0.003*\frac{20.1-6.03}{6.03}=0.007>0.005\text{ OK}

If you do not reduce the value of ${{\rho }_{\max }}$ then It becomes exactly 0.005 or maybe less. This means the reduction factor 𝛟 = 0.9 it doesn’t applicable. So you must reduce the ${{\rho }_{\max }}$ value as ${{\rho }_{design}}$ .

Step 9: Rebar calculation & Detailing

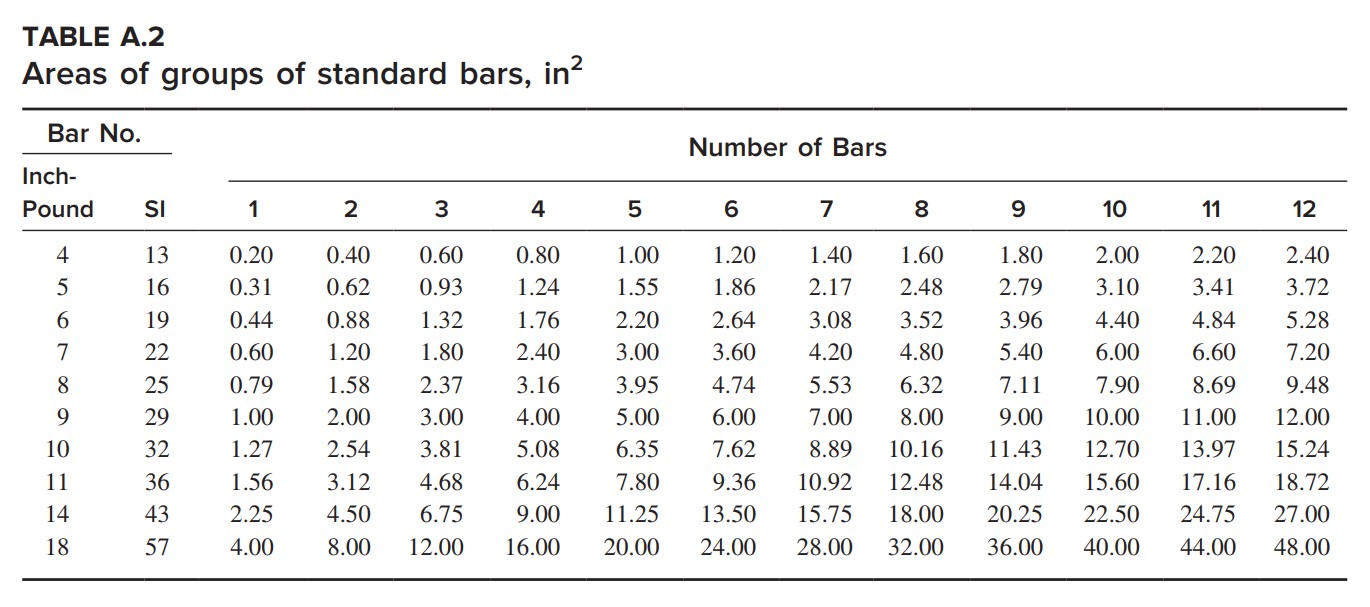
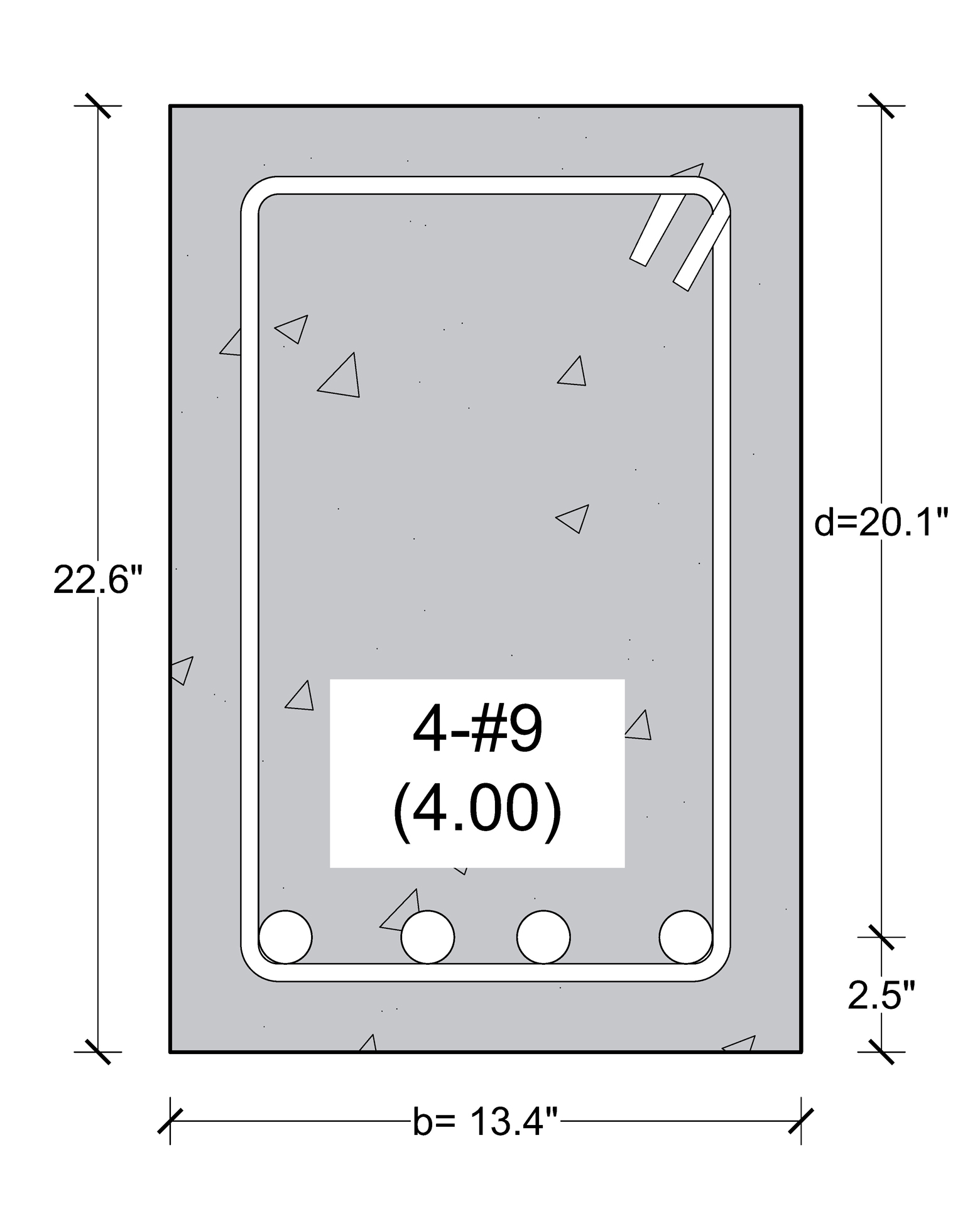
Used 4-#9 (4.00 in²) bar

{{A}_{s,provide}}(4.00\text{ }i{{n}^{2}})>{{A}_{s,required}}(3.90\text{ }i{{n}^{2}})\text{ OK}

Assuming 2.5 in. concrete cover from the centroid of the bars,
h = d+2.5” = 20.1+2.5=22.6 inch
Beam Size:
b=13.4 inch
h=22.6 inch

Reference

Design of Concrete Structures Sixteenth Edition by David Drawin & Charles W. Dolan.
Building Code Requirements for Structural Concrete (ACI 318-19)
ASCE 7_22 Minimum Design Loads and Associated Criteria for Buildings

Check this Beam Design Calculator ACI 318-19

See more Article:

CIVILHEX

The Hub of Engineering eXploration

Have you ever stared at a towering skyscraper and wondered how it stays defying gravity? Or marveled at the intricate network of bridges and roads that keep our cities humming? If the world of civil engineering sparks your curiosity, then welcome to CIVILHEX, your ultimate hub of engineering exploration!

Beam Design – Tension Reinforcement (Unknown Cross-Section) ACI 318-19

Solution

Reference

Falling Head and Constant Head Method Permeability Test

Beam Design Calculator ACI 318-19 – Tension Reinforcement (Unknown Cross-Section)

Related Posts

Leave a Reply Cancel reply

Popular Article

Browse by Category

Contact Us

Location

Newsletter

Welcome Back!

Retrieve your password

Add New Playlist