Traffic Design-An Accident Investigation Problem

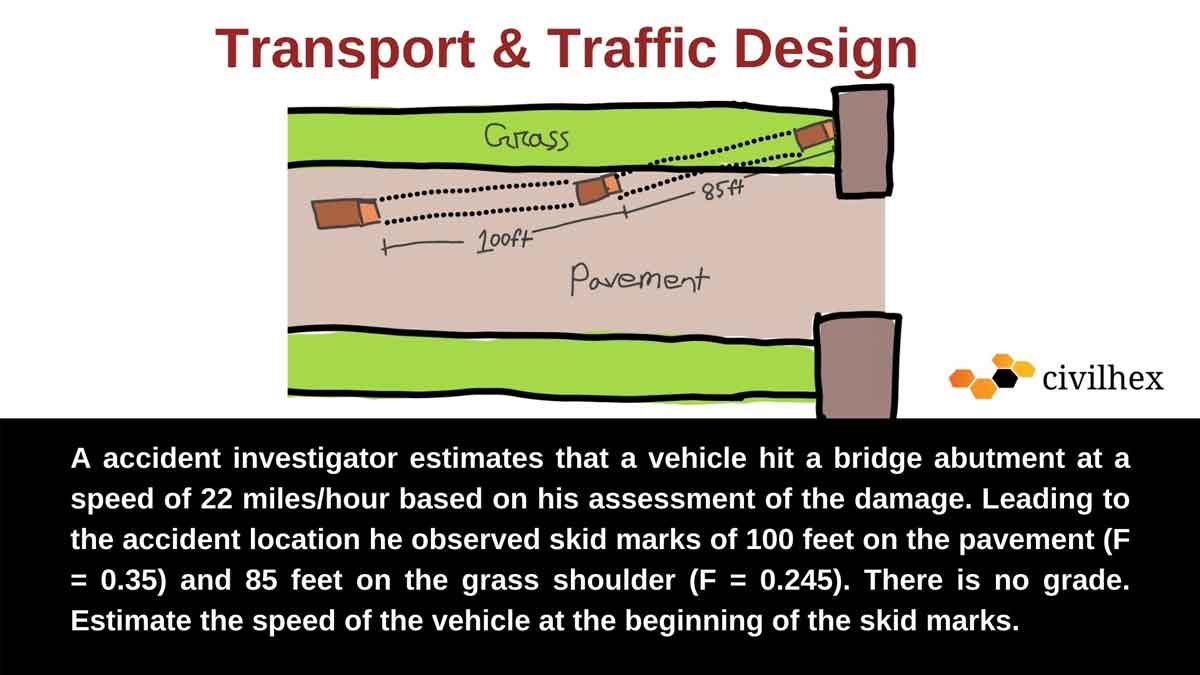
An accident investigator estimates that a vehicle hit a bridge abutment at a speed of 22 miles/hour based on his assessment of the damage. Leading to the accident location he observed skid marks of 100 feet on the pavement (F = 0.35) and 85 feet on the grass shoulder (F = 0.245). There is no grade. Estimate the speed of the vehicle at the beginning of the skid marks.

Transport & Traffic Design-A Accident Investigation Problem

Solution:

Given:

{{V}_{f}}=22\text{ miles/hr} \\ {{d}_{b\text{ }(pavement)}}\text{=100 feet and }F=\text{ }0.35 \\ {{d}_{b\text{ }(grass)}}=\text{85 feet and }F=\text{ }0.245 \\ \text{Now} \\ {{d}_{b\text{ }(grass)}}=\frac{{{V}_{i}}^{2}-{{V}_{f}}^{2}}{30(F)} \\ \Rightarrow 85=\frac{{{V}_{i}}^{2}-{{22}^{2}}}{30(0.245)} \\ {{V}_{i\text{ }(grass)}}=33.30\text{ miles/hr} \\ \text{Again,} \\ {{d}_{b\text{ }(pavement)}}=\frac{{{V}_{i}}^{2}-{{V}_{f}}^{2}}{30(F)} \\ \Rightarrow 100=\frac{{{V}_{i}}^{2}-{{33.30}^{2}}}{30(0.35)}\text{ }\to \text{ }\because \text{ }{[{V}_{i(grass)}}={{V}_{f(pavement)}]} \\ \therefore {{V}_{i(pavement)}}=46.46\text{ miles/hr}

The speed of the vehicle at the beginning of the skid marks is 46.46 miles/hr.

CIVILHEX

Inspiring Civil Engineers & Architects with a Treasure Trove of Information and Ideas!

Welcome to Civilhex, your ultimate online destination for civil engineers, structural engineers, architects, construction professionals, and civil engineering students. Explore various engineering topics, ranging from geotechnical, structural, foundation water resources, and transportation engineering. Stay up-to-date with the latest advancements in technology, cutting-edge research, comprehensive guides, and safety-related information. Civilhex is your go-to resource for all things civil engineering. Visit us today and enhance your knowledge in the field.

Traffic Design-An Accident Investigation Problem

Transport & Traffic Design-A Accident Investigation Problem

Related Posts

Discussion about this post

Popular Article

Recent News

Browse by Category

Contact Us

Location

Recent News

Welcome Back!

Retrieve your password

Add New Playlist